Сравнение концентраций ИЛ-6 в плазме больных COVID-19 в зависимости от исхода заболевания¶
А.С. Смирнов1, З.Р. Коробова2
1 - Кафедра биоинформатики МБФ РНИМУ им. Н.И. Пирогова
2 - Лаборатория молекулярной иммунологии НИИЭМ им. Пастера
Работа выполнена на базе Лаборатория молекулярной иммунологии НИИЭМ им. Пастера в рамках Летней школы "Наука - врачам будущего" 4-19 июля 2022 года
Научный руководитель - З.Р. Коробова
Дата составления отчета - 18 сентября 2022 года
Введение¶
COVID-19 — опасное инфекционное заболевание, вызываемое вирусом SARS-CoV-2 из рода Betacoronavirus1. Для этого заболевания характерны тяжелые поражения лёгких вследствие атипичной пневмонии и сравнительно высокая летальность, особенно у лиц старшей возрастной группы (старше 50 лет)2. В качестве основной причины смерти выделяют неадекватный иммунный ответ на возбудителя — цитокиновый шторм3. Цитокины — это большая группа гликопротеиновых молекул, отвечающая за гуморальную регуляцию жизнедеятельности клеток. С их помощью осуществляется межклеточное и межсистемное взаимодействие. Цитокины делят на две большие группы: провоспалительные и противовоспалительные. В литературе4 существуют данные, что концентрация провоспалительных цитокинов в плазме крови может быть важным прогностическим фактором. Цель нашего исследования: проверить, может ли являться концентрация интерлейкина-6, одного из главных провоспалительных цитокинов, в плазме крови прогностическим фактором исхода у больных старшей возрастной группы.
Уровень значимости при проверке гипотез = 0.05
Априорные гипотезы¶
Первая
- Н0: Средний уровень IL-6 у умерших равен таковому у выписывшихся пациентов
- Н1: Средний уровень IL-6 у умерших выше таковому у выписывшихся пациентов
Вторая
- Н0: Средний уровень IL-6 у выписывшихся равен таковому у здоровых
- Н1: Средний уровень IL-6 у выписывшихся выше таковому у здоровых
Третья
- Н0: Средний уровень IL-6 у больных равен таковому у здоровых пациентов
- Н1: Средний уровень IL-6 у больных выше таковому у здоровых пациентов
Апостериорные гипотезы¶
- Результаты, полученные с помощью метода иммуноферментного анализа (набор Вектор Бест, Новосибирск, Россия), сопоставимы с результатами, полученными с помощью метода мультиплесного анализа Luminex Magpix (набор для определения 47 цитокинов и ростовых факторов, Millipore, Burlington, Massachusetts).
- Присутствует корреляция уровня ИЛ-6 с возрастом
- Различия в концентрациях ИЛ-6 в группах, с разной степенью тяжести
- Н0: Средний уровень IL-6 у больных с разной степенью тяжести не отличается
- Н1: Средний уровень IL-6 у больных с разной степенью тяжести отличается
Дизайн эксперимента¶
Материалы¶
Образцы крови были получены от пациентов, проходивших лечение в СЗОНКЦ им. Л.Г. Соколова ФМБА России на базе инфекционного COVID-специализированного отделения. Всем пациентам впервые был установлен диагноз "COVID-19" (U07.1), подтвержденный c помощью качественного ПЦР. Сбор периферической крови для образцов осуществлялся в пробирки с ЭДТА в приёмном покое. Для отделения плазмы осуществлялось центрифугирование образцов при 350g в течение 10 мин. В дальнейшем образцы плазмы замораживались при температуре -80C.
От всех пациентов было получено информированное добровольное согласие, исследование проводилось в соответствии с Хельсинской декларацией; проведение исследования было одобрено этическим комитетом СЗОНКЦ.
Методы¶
Определение уровня ИЛ-6 проводилось двумя методами:
- Методом ИФА на наборе Интерлейкин-6-ИФА-БЕСТ (Вектор Бест, Новосибирск, Россия) в соответствии с инструкцией производителя. Для регистрации результатов был использован ИФА анализатор Multiskan FC (Thermo Scientific, MA, USA).
- Методом мультиплексного анализа по технологии xMAP (Luminex, Austin, Texas), для определения цитокинов использовался набор для определения 47 цитокинов и ростовых факторов (Millipore, Burlington, Massachusetts).
Cтатистическая обработка данных была выполнена с помощью языка программирования Python.
Версия Python
import sys
print(sys.version)
Версии используемых библиотек
import pandas as pd
import datetime
import seaborn as sns
import matplotlib
import matplotlib.pyplot as plt
import scipy as sp
import statsmodels.api as sm
print("pandas = " + pd.__version__)
print("seaborn = " + sns.__version__)
print("matplotlib = " + matplotlib.__version__)
print("scipy = " + sp.__version__)
print("statsmodels = " + sm.__version__)
Критерии включения¶
- Возраст пациента от 50 до 70 лет включительно
- Госпитализация на 5-10 сутки заболевания
Критерии исключения¶
- Наличие перенесенного COVID-19 или соответствующей вакцинации в анамнезе
- Выявленный геновариант “Омикрон”
- Наличие иммуннокомпрометирующих состояний: беременность, онкологические заболевания, хронические заболевания в стадии обострения, аутоиммунные и аутовоспалительные заболевания, гепатиты В, С, ВИЧ-инфекция
Отбор пациентов¶
pd.set_option('display.max_columns', 500)
data = pd.read_excel("~/Documents/Piter/Immunology/tables/raw_Patients_data.xlsx")
print(data.shape)
data.head()
Проверка дат¶
for i in data.index:
if not (isinstance(data.loc[i, "Manifistation_Date"],datetime.date) and isinstance(data.loc[i, "Hospitalization_Date"],datetime.date)):
data.drop(index = i, inplace = True)
data.shape
data = data[data["Manifistation_Date"] < data["Hospitalization_Date"]]
data.shape
Проверка по критериям включения¶
data = data[(data["Disease_Day"] >= 5) & (data["Disease_Day"] <= 10)]
data.shape
Примечание: изначально планировалось брать пациентов с 40 лет, но не набралось достаточное количество образцов с достаточным количеством плазмы. Поэтому отбор образцов ниже проводился с 40 лет, но потом вручную были исключены пациенты моложе 50 лет
# сначала планировалась брать пациентов с 40 лет, но не нашлось достаточное количество образцов
data = data[(data["Age"] >= 40) & (data["Age"] <= 70)]
data.shape
Проверка по критериям исключения¶
data = data[(data["Full_Vaccination"] == 0) & (data["Second_Component_Date"].isna()) & (data["Vaccine_Code"].isna()) & (data["Days_Beetween_Vaccination_Disease"].isna())]
data.shape
data = data[(data["Omicron"] == 0) | (data["Omicron"].isna())]
data.shape
Факторизация исходов¶
data["Outcome"].value_counts()
data.loc[data['Outcome'].str.contains("выписан"),"Outcome"] = "выписка"
data.loc[data['Outcome'].str.contains("амбул"),"Outcome"] = "амбулаторно"
data.loc[data['Outcome'].str.contains("умер"),"Outcome"] = "смерть"
data.loc[data['Outcome'].str.contains("реаб"),"Outcome"] = "реабилитация"
data["Outcome"].value_counts()
Формирование групп¶
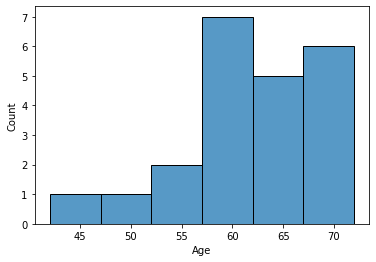
Необходимо, чтобы распределения возраста и пола в группах примерно совпадали по форм. Группа пациентов с благоприятным исходом несколько превосходила группу с неблагоприятным исходом по количество образцов.
sns.histplot(data.loc[data["Outcome"] == "смерть","Age"],binwidth = 5)
data.loc[data["Outcome"] == "смерть","Age"].value_counts().sort_index()
favorable = data[(data["Outcome"] == "выписка") | (data["Outcome"] == "реабилитация")]
favorable["Age"].value_counts().sort_index()
# необходимо было отобрать в 3 раза больше образцов, чем нужно, так как не было известно,
# какие образцы есть в достаточном количестве
k = 3
# Случайный выбор образцов из возрастных групп
age40_45 = favorable[(favorable["Age"] > 40) & (favorable["Age"] <= 45)].sample(n = 1 * k,random_state = 555)
age45_50 = favorable[(favorable["Age"] > 45) & (favorable["Age"] <= 50)].sample(n = 1 * k,random_state = 555)
age50_55 = favorable[(favorable["Age"] > 50) & (favorable["Age"] <= 55)].sample(n = 2 * k,random_state = 555)
age55_60 = favorable[(favorable["Age"] > 55) & (favorable["Age"] <= 60)].sample(n = 6 * k,random_state = 555)
age60_65 = favorable[(favorable["Age"] > 60) & (favorable["Age"] <= 65)].sample(n = 5 * k,random_state = 555)
age65_70 = favorable[(favorable["Age"] > 65) & (favorable["Age"] <= 70)].sample(n = 7 * k,random_state = 555)
sample_favor = pd.concat([age40_45,age45_50,age50_55,age55_60,age60_65,age65_70],axis = 0)
sample_favor["Age"].value_counts().sort_index()
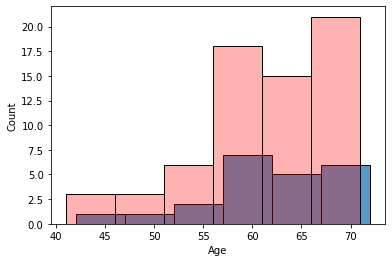
Распределение по возрасту в выборке совпало с исходной генеральной совокупностью.
sns.histplot(data.loc[data["Outcome"] == "смерть","Age"], binwidth = 5)
sns.histplot(sample_favor["Age"],binwidth = 5,color = "red",alpha = 0.3)
print("Количество образцов = " + str(len(sample_favor.index)))
К сожалению, распределение по полу не удалось сделать равномерным, но мы постарались минимизировать различия.
sample_favor["Sex"].value_counts()
Сохраняем списки¶
final = pd.concat([data[data["Outcome"] == "смерть"],sample_favor])
final = final[["ID","Outcome","Age", "Sex"]].sort_values(by = ["Outcome","Age","Sex"])
final.head()
final[(final["Sex"] == 1) & (final["Outcome"] == "выписка")].sort_values(by = "Age").to_excel("~/Documents/Piter/Immunology/surv_men.xlsx",index = False)
final[(final["Sex"] == 2) & (final["Outcome"] == "выписка")].sort_values(by = "Age").to_excel("~/Documents/Piter/Immunology/surv_women.xlsx",index = False)
final[(final["Sex"] == 1) & (final["Outcome"] == "смерть")].sort_values(by = "Age").to_excel("~/Documents/Piter/Immunology/dead_men.xlsx",index = False)
final[(final["Sex"] == 2) & (final["Outcome"] == "смерть")].sort_values(by = "Age").to_excel("~/Documents/Piter/Immunology/dead_women.xlsx",index = False)
Также вручную были отобраны образцы 8 здоровых людей так, чтобы распределение по полу и возрасту соответствовали опытным группам.
Эксперимент¶
Поиск образцов¶
plan = pd.read_excel("~/Documents/Piter/Immunology/tables/planning_elisa.xlsx", sheet_name="Список образцов", header = [0,1])
plan
Разметка планшета и результат¶
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | калибратор1 | 910_1 | 191_1 | 313_1 | 174_1 | 770_1 | 542_1 | 898а_1 | 607_1 | 280_1 | зд1_1 | зд5_1 |
| B | калибратор2 | 910_2 | 70_2 | 313_2 | 174_2 | 770_2 | 542_2 | 898а_2 | 607_2 | 280_2 | зд1_2 | зд5_2 |
| C | калибратор3 | 464_1 | 129_1 | 540_1 | 432_1 | 226_1 | 1126_1 | 1129_1 | 1087_1 | 809_1 | зд2_1 | зд6_1 |
| D | калибратор4 | 464_2 | 129_2 | 540_2 | 432_2 | 226_2 | 1126_2 | 1129_2 | 1087_2 | 809_2 | зд2_2 | зд6_2 |
| E | калибратор5 | 110_1 | 865_1 | 822_1 | 165_1 | 1153_1 | 774_1 | 238_1 | 1077_1 | 998_1 | зд3_1 | зд7_1 |
| F | калибратор6 | 110_2 | 865_2 | 822_2 | 165_2 | 1153_2 | 774_2 | 238_2 | 1077_2 | 998_2 | зд3_2 | зд7_2 |
| G | контроль | 7_1 | 356_1 | 546_1 | 790_1 | 1094_1 | 55_1 | 689_1 | 351_1 | 605_1 | зд4_1 | зд8_1 |
| H | 70_1 | 7_2 | 356_2 | 546_2 | 790_2 | 1094_2 | 55_2 | 689_2 | 351_2 | 605_2 | зд4_2 | зд8_2 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | 94,23 | 65,35 | 52,7 | 46,57 | 73,58 | 34,15 | 150,9 | 34,73 | 40,8 | 6,815 | 11,78 | |
| B | 43,04 | 54,35 | 52,85 | 48,7 | 73,07 | 30,57 | 142 | 35,22 | 42,31 | 7,806 | 12,84 | |
| C | 39,49 | 133,3 | 39,96 | 38,61 | 7,302 | 8,317 | 23,55 | 47,04 | 210,4 | 8,691 | 7,111 | |
| D | 37,82 | 155,1 | 42,34 | 44,5 | 7,424 | 7,446 | 28 | 45,32 | 141,2 | 10,03 | 5,004 | |
| E | 17,86 | 10,91 | 11,18 | 60,07 | 72,61 | 34,25 | 45,68 | 44,8 | 60,05 | 8,37 | 4,788 | |
| F | 21,03 | 16,38 | 16,02 | 48,2 | 44,25 | 31,1 | 36,73 | 38,17 | 54,74 | 9,677 | 4,937 | |
| G | 65,07 | 30,68 | 37,25 | 56,83 | 65,81 | 24,26 | 26,29 | 49,21 | 28,9 | 26,17 | 10,4 | 5,281 |
| H | 51,69 | 31,13 | 32,89 | 57,87 | 41,14 | 29,4 | 24,84 | 65,47 | 44,88 | 32,18 | 21,62 | 25,78 |
Единицы измерения - пг/мл. Все образцы сделаны в дублях, за исключением одного (№191) из-за недостаточности плазмы. Ретроспективно мы добавили результаты оценки концентраций IL-6 с помощью технологии xMAP.
Обработка результатов¶
Описательная статистика¶
Сопоставление данных пациентов с результатами¶
results = pd.read_excel("~/Documents/Piter/Immunology/tables/results.ods",engine = "odf",index_col = 0)
results.head()
samples = pd.read_excel("~/Documents/Piter/Immunology/tables/samples.ods",engine = "odf",index_col = 0)
samples.head()
for i in results.index:
results.loc[i,"Outcome"] = samples.loc[i,"Outcome"]
results.loc[i,"Age"] = samples.loc[i,"Age"]
results.loc[i,"Sex"] = samples.loc[i,"Sex"]
results.head()
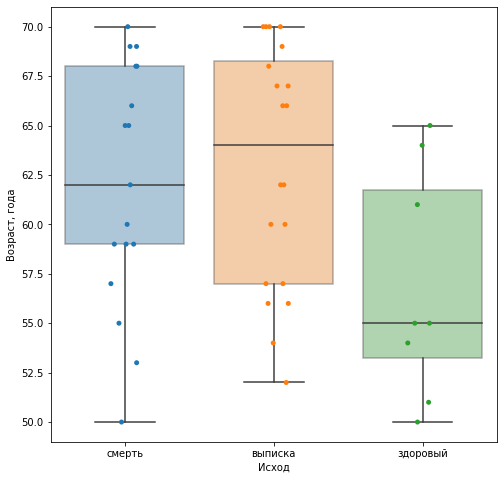
Распределение по полу и возрасту¶
fig,ax = plt.subplots(figsize = (8,8))
sns.boxplot(data=results, x="Outcome", y="Age", boxprops={'alpha': 0.4},ax = ax,showfliers = False)
sns.stripplot(data=results, x="Outcome", y="Age", dodge=True, ax=ax)
ax.set_xlabel("Исход")
ax.set_ylabel("Возраст, года")
| Группа | Мужчины (n = 21) | Женщины (n = 24) |
|---|---|---|
| Выписка (n = 20) | 9 | 11 |
| Смерть (n = 17) | 9 | 8 |
| Здоровые (n = 8) | 3 | 5 |
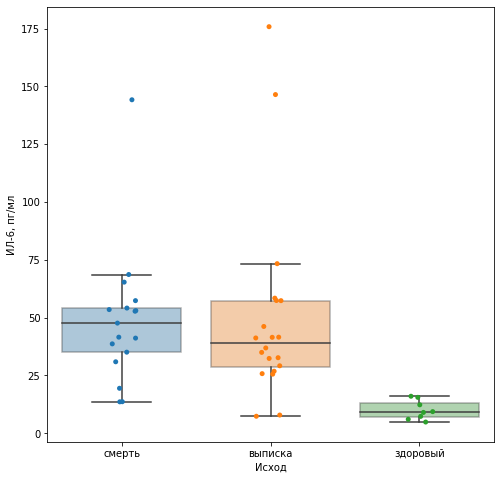
Результаты¶
fig,ax = plt.subplots(figsize = (8,8))
sns.boxplot(data=results, x="Outcome", y="Mean, pg/ml", boxprops={'alpha': 0.4},ax = ax,showfliers = False)
sns.stripplot(data=results, x="Outcome", y="Mean, pg/ml", dodge=True, ax=ax)
ax.set_xlabel("Исход")
ax.set_ylabel("ИЛ-6, пг/мл")
plt.savefig("res.png",dpi = 300)
r1 = results.copy()
for i in r1.index:
if samples.loc[i,"Outcome"] == "здоровый":
r1.loc[i,"Outcome"] = samples.loc[i,"Outcome"]
else:
r1.loc[i,"Outcome"] = "больной"
r1.loc[i,"Age"] = samples.loc[i,"Age"]
r1.loc[i,"Sex"] = samples.loc[i,"Sex"]
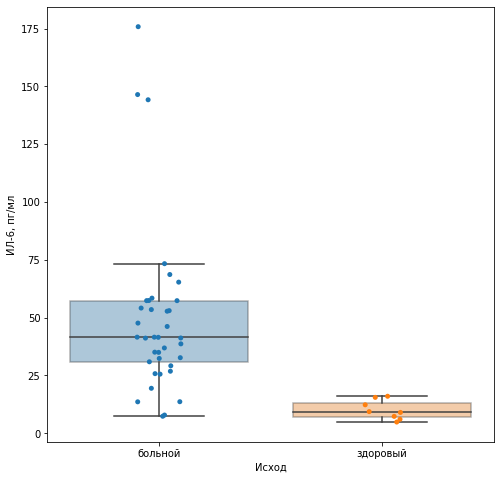
fig,ax = plt.subplots(figsize = (8,8))
sns.boxplot(data=r1, x="Outcome", y="Mean, pg/ml", boxprops={'alpha': 0.4},ax = ax,showfliers = False)
sns.stripplot(data=r1, x="Outcome", y="Mean, pg/ml", dodge=True, ax=ax)
ax.set_xlabel("Исход")
ax.set_ylabel("ИЛ-6, пг/мл")
plt.savefig("il6_1.png",dpi = 300)
Проверка априорных гипотез¶
Проверка на нормальность распределения¶
Результаты проверки зависят от того считаем ли мы уровень ИЛ-6 > 125 пг/мл выбросами.
Если не считаем¶
dead_with_high = results.loc[(results["Outcome"] == "смерть"),"Mean, pg/ml"]
survive_with_high = results.loc[(results["Outcome"] == "выписка"),"Mean, pg/ml"]
sick_with_high = results.loc[((results["Outcome"] == "смерть") | (results["Outcome"] == "выписка")),"Mean, pg/ml"]
healthy_with_high = results.loc[(results["Outcome"] == "здоровый"),"Mean, pg/ml"]
print(sp.stats.shapiro(dead_with_high))
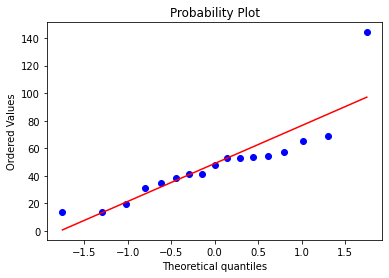
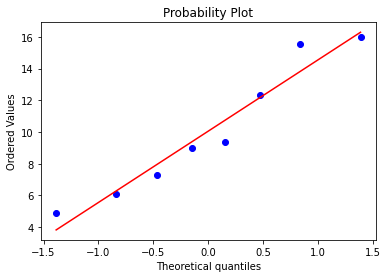
sp.stats.probplot(dead_with_high,plot = plt)
print(sp.stats.shapiro(survive_with_high))
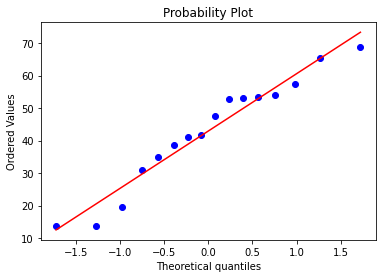
sp.stats.probplot(survive_with_high,plot = plt)
print(sp.stats.shapiro(sick_with_high))
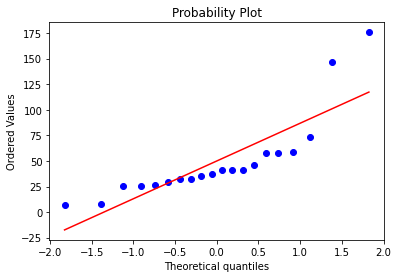
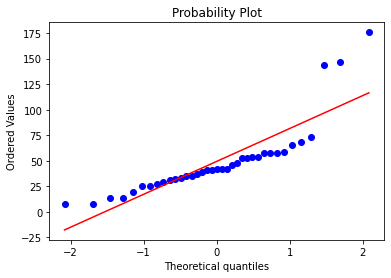
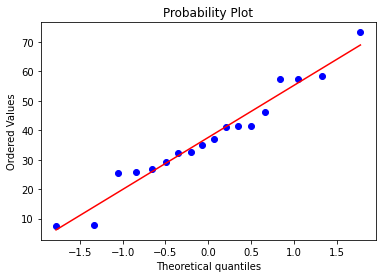
sp.stats.probplot(sick_with_high,plot = plt)
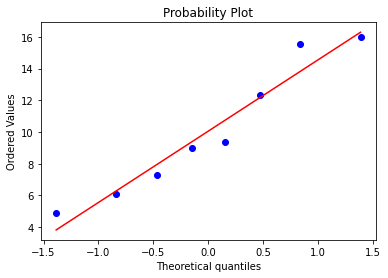
print(sp.stats.shapiro(healthy_with_high))
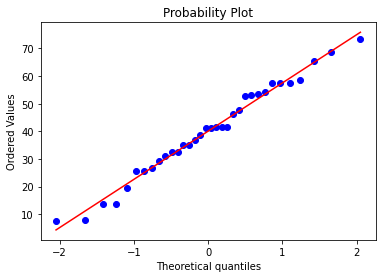
sp.stats.probplot(healthy_with_high,plot = plt)
Если считаем¶
dead_without_high = results.loc[(results["Outcome"] == "смерть") & (results["Mean, pg/ml"] < 125),"Mean, pg/ml"]
survive_without_high = results.loc[(results["Outcome"] == "выписка") & (results["Mean, pg/ml"] < 125),"Mean, pg/ml"]
sick_without_high = results.loc[((results["Outcome"] == "смерть") | (results["Outcome"] == "выписка")) & (results["Mean, pg/ml"] < 125),"Mean, pg/ml"]
healthy_without_high = results.loc[(results["Outcome"] == "здоровый") & (results["Mean, pg/ml"] < 125),"Mean, pg/ml"]
print(sp.stats.shapiro(dead_without_high))
sp.stats.probplot(dead_without_high,plot = plt)
print(sp.stats.shapiro(survive_without_high))
sp.stats.probplot(survive_without_high,plot = plt)
print(sp.stats.shapiro(sick_without_high))
sp.stats.probplot(sick_without_high,plot = plt)
print(sp.stats.shapiro(healthy_without_high))
sp.stats.probplot(healthy_without_high,plot = plt)
Если мы считаем высокие значения ИЛ-6 выбросами, то все группы имеют нормальное распределение. Если нет, только группа здоровых имеет нормальное распределение, хотя малая величина группы позволяет сомневаться в этом. Гипотезы будут проверены как параметрическими критериями, так и непараметрическими. Мы рекомендуем использовать в качестве референтных непараметрические критерии.
Проверка статистическим критерием¶
sp.stats.mannwhitneyu(dead_with_high, survive_with_high, use_continuity = True, alternative = "greater")
sp.stats.ttest_ind(dead_without_high, survive_without_high, alternative = "greater", random_state = 555)
sp.stats.mannwhitneyu(survive_with_high, healthy_with_high, use_continuity = True, alternative = "greater")
sp.stats.ttest_ind(survive_without_high, healthy_without_high, alternative = "greater", random_state = 555)
sp.stats.mannwhitneyu(sick_with_high, healthy_with_high, use_continuity = True, alternative = "greater")
sp.stats.ttest_ind(sick_without_high, healthy_without_high, alternative = "greater", random_state = 555)
Несмотря на споры по поводу вида распределения, выбор критерия не влияет на конечный результат. Визуально видно, что поправки на множественное сравнения также не повлияют на результат.
Выводы¶
- ИЛ-6 участвует в воспалительном процессе при COVID-19.
- Эксперимент проведен корректно, так как уровень ИЛ-6 в плазме крови у здоровых больных меньше, чем у больных: как умерших, так и выздоровевших.
- ИЛ-6 изолированно не может использоваться для прогноза исхода заболевания.
Проверка апостериорных гипотез¶
Результаты ИФА и MAGPIX
result = pd.read_excel("~/Documents/Piter/Immunology/tables/results_xmap_and_vector.xlsx")
result.head()
Сопоставимость методов¶
Сопоставимость методов будем смотреть следующими способами:
- Коэффициент корреляции Спирмена. Применение коэффициента корреляции для сравнения двух методов не вполне корректно, но ввиду распространенности этого метода в медицинской и технической литературе мы выбрали включить его в анализ.
- Тест Вилкоксона
- График Бланда-Альтмана5
- Регрессия Пассинга-Баблока6,7
MAGPIX условно считается референсным, так как эксперимент с этой тест-системой выполнялся на более свежих образцах плазмы более опытным экспериментатором
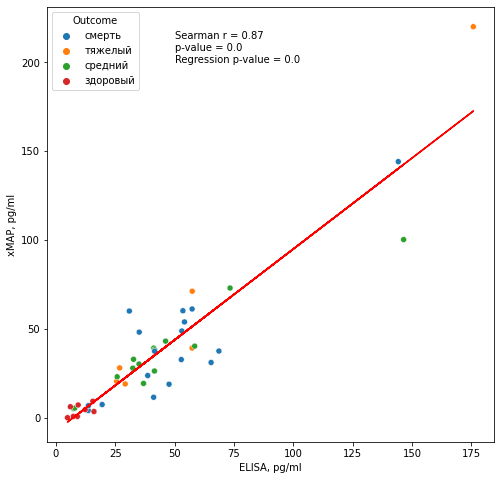
Коэффициент корреляции Спирмена¶
fig, ax = plt.subplots(figsize = (8,8))
elisa_spearman, elisa_p = sp.stats.spearmanr(a = result["ELISA, pg/ml"], b = result["xMAP, pg/ml"])
res = sp.stats.linregress(x = result["ELISA, pg/ml"],y = result["xMAP, pg/ml"])
text = "Searman r = " + str(round(elisa_spearman,2)) + "\n" + "p-value = " + str(round(elisa_p,5)) + "\nRegression p-value = " + str(round(res.pvalue,5))
sns.scatterplot(data = result, x = "ELISA, pg/ml", y = "xMAP, pg/ml", hue = "Outcome", ax =ax)
x = result["ELISA, pg/ml"]
y = res.intercept + res.slope*result["ELISA, pg/ml"]
plt.plot(x, y, 'r', label='fitted line')
plt.text(50,200,text)
Тест Вилкоксона¶
sp.stats.wilcoxon(result["ELISA, pg/ml"], result["xMAP, pg/ml"], correction = True)
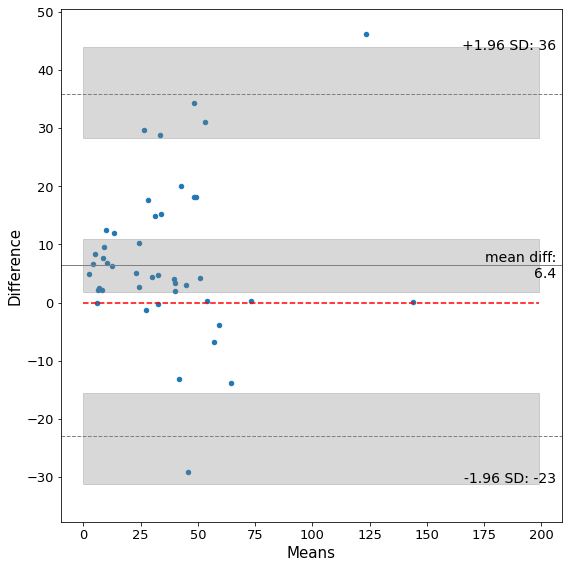
График Бланда-Альтмана¶
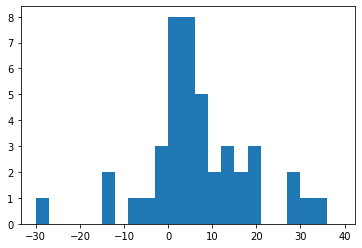
Для графика Бланда-Альтмана необходимо, чтобы разница между двумя методами была распределена нормально.
result["Diff"] = result["ELISA, pg/ml"] - result["xMAP, pg/ml"]
plt.hist(result["Diff"], bins=range(-30,40,3))
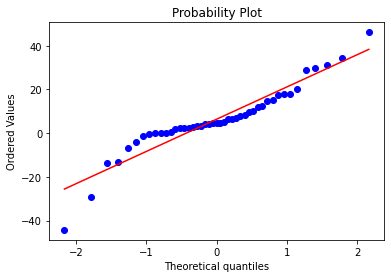
sp.stats.shapiro(result["Diff"])
sp.stats.probplot(result["Diff"],plot = plt)
Как можно видеть, распределение разницы между двумя методами распределено не по нормальному закону. Мы применим преобразование, сводящее распределение к нормальному, взяв квадратный корень от значений концентрации. Однако поскольку корень из концентраций несет исключительно математическое значение, и не имеет биологического смысла, мы дополнительно прилагаем график и для неизменных концентраций.
Обычные остатки¶
fig, ax = plt.subplots(figsize = (8,8))
#result["sqrt_Vector"] = np.sqrt(result["Mean, pg/ml"])
#result["sqrt_xMAP"] = np.sqrt(result["xMAP, pg/ml"])
#result["delta_sqrt"] = result["sqrt_Vector"] - result["sqrt_xMAP"]
#sp.stats.shapiro(result["delta_sqrt"])
t = sp.stats.t(df = len(result.index) - 1).ppf(0.975)
se_mean = np.std(result["Diff"]) / np.sqrt(len(result.index))
se_limit = np.std(result["Diff"]) * np.sqrt(3) / np.sqrt(len(result.index))
sm.graphics.mean_diff_plot(result["ELISA, pg/ml"],result["xMAP, pg/ml"], ax = ax)
x = list(range(0,200))
upper = result["Diff"].mean() + result["Diff"].std() * 1.96
lower = result["Diff"].mean() - result["Diff"].std() * 1.96
plt.plot(x,np.repeat(0,len(x)),color = "r", linestyle = "--")
ax.fill_between(x, np.repeat(result["Diff"].mean() - t*se_mean,len(x)), np.repeat(result["Diff"].mean() + t*se_mean,len(x)), color = "grey", alpha = 0.3)
ax.fill_between(x, np.repeat(upper - t*se_limit,len(x)), np.repeat(upper + t*se_limit,len(x)), color = "grey", alpha = 0.3)
ax.fill_between(x, np.repeat(lower - t*se_limit,len(x)), np.repeat(lower + t*se_limit,len(x)), color = "grey", alpha = 0.3)
plt.plot()
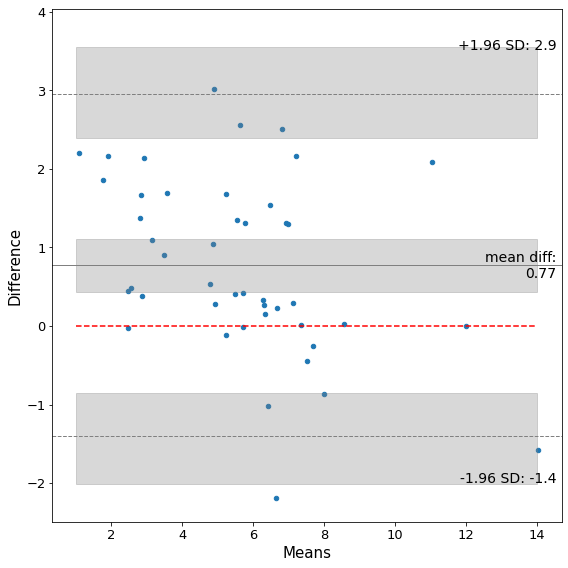
Корень из остатков¶
result["sqrt_Vector"] = np.sqrt(result["ELISA, pg/ml"])
result["sqrt_xMAP"] = np.sqrt(result["xMAP, pg/ml"])
result["delta_sqrt"] = result["sqrt_Vector"] - result["sqrt_xMAP"]
print(sp.stats.shapiro(result["delta_sqrt"]))
t = sp.stats.t(df = len(result.index) - 1).ppf(0.975)
se_mean = np.std(result["delta_sqrt"]) / np.sqrt(len(result.index))
se_limit = np.std(result["delta_sqrt"]) * np.sqrt(3) / np.sqrt(len(result.index))
fig, ax = plt.subplots(figsize = (8,8))
sm.graphics.mean_diff_plot(result["sqrt_Vector"],result["sqrt_xMAP"], ax = ax)
x = list(range(1,15))
upper = result["delta_sqrt"].mean() + result["delta_sqrt"].std() * 1.96
lower = result["delta_sqrt"].mean() - result["delta_sqrt"].std() * 1.96
plt.plot(x,np.repeat(0,len(x)),color = "r", linestyle = "--")
ax.fill_between(x, np.repeat(result["delta_sqrt"].mean() - t*se_mean,len(x)), np.repeat(result["delta_sqrt"].mean() + t*se_mean,len(x)), color = "grey", alpha = 0.3)
ax.fill_between(x, np.repeat(upper - t*se_limit,len(x)), np.repeat(upper + t*se_limit,len(x)), color = "grey", alpha = 0.3)
ax.fill_between(x, np.repeat(lower - t*se_limit,len(x)), np.repeat(lower + t*se_limit,len(x)), color = "grey", alpha = 0.3)
plt.show()
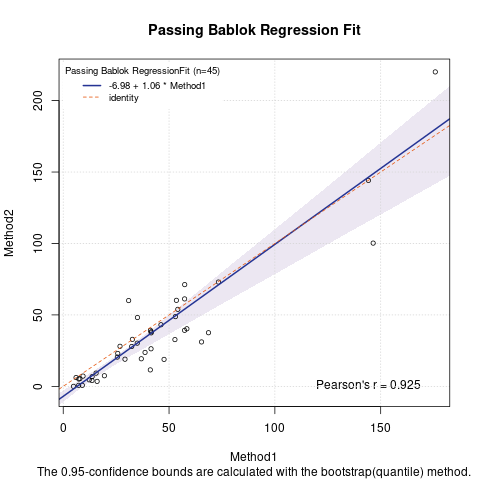
Регрессия Пассинга-Баблока¶
import rpy2
%load_ext rpy2.ipython
print(rpy2.__version__)
%%R
install.packages("mcr")
install.packages("cellranger")
install.packages("readxl")
%%R
print(R.version)
%%R
print(packageVersion("mcr"))
%%R
library(mcr)
data = as.data.frame(readxl::read_excel("~/Documents/Piter/Immunology/tables/results_xmap_and_vector.xlsx"))
head(data)
%%R
PB.reg <- mcreg(as.numeric(data[,"ELISA, pg/ml"]),as.numeric(data[,"xMAP, pg/ml"]), method.reg = "PaBa")
PB.reg@para
%%R
plot(PB.reg)
%%R
printSummary(PB.reg)
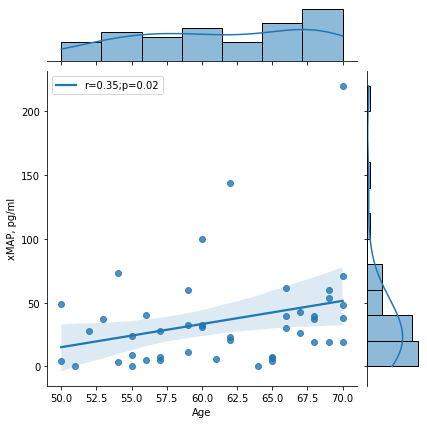
Корреляция ИЛ-6 с возрастом¶
r, p = sp.stats.spearmanr(a = result["Age"], b = result["xMAP, pg/ml"])
ax = sns.jointplot(data = result, x = "Age", y = "xMAP, pg/ml", kind="reg", line_kws={'label':"r={:.2f};p={:.2f}".format(r,p)})
ax.ax_joint.legend()
Сравнение уровня ИЛ-6 у больных с разной степенью тяжести¶
disease = result[result["Outcome"] != "здоровый"]
print(disease.shape)
disease["Outcome"].value_counts()
dead = disease.loc[disease["Outcome"] == "смерть", "xMAP, pg/ml"]
moderate = disease.loc[disease["Outcome"] == "средний", "xMAP, pg/ml"]
severe = disease.loc[disease["Outcome"] == "тяжелый", "xMAP, pg/ml"]
sp.stats.kruskal(dead,moderate,severe)
sp.stats.mannwhitneyu(dead,moderate)
sp.stats.mannwhitneyu(severe,moderate)
sp.stats.mannwhitneyu(severe,dead)
Выводы¶
- Методы ИФА и MAGPIX в целом сопоставимы, но имеется статистически значимое смещение результатов одного метода над другим: у ИФА завышенные результаты относительно MAGPIX
- Присутствует статистически значимая корреляция уровня ИЛ-6 в плазме крови с возрастом
- Уровень ИЛ-6 не отличается в группах с различной тяжестью заболевания
Выводы¶
ИЛ-6 не может изолированно использоваться ни для прогноза исхода заболевания, ни степени тяжести. Методы ИФА и MAGPIX сопоставимы для определения ИЛ-6 в плазме, пусть и с некоторой систематической ошибкой. Концентрация ИЛ-6 в плазме коррелирует с возрастом пациентов.
Обсуждения¶
В ходе обработки результатов, мы столкнулись с двумя лимитирующими факторами:
- Постановка иммуноферментного анализа и мультиплексного анализа выполнялась в технически различающихся условиях.
- В наше исследование включены образцы с генетически подтвержденным вариантом Дельта (B1.617.2). Возможно, полученные нами результаты не будут в полной мере применимы к другим геновариантам вируса.
Библиография¶
P, N., R, N., B, V., S, R., & A, S. (2022). COVID-19: Invasion, pathogenesis and possible cure - A review. Journal of virological methods, 300, 114434. https://doi.org/10.1016/j.jviromet.2021.114434
Siordia J. A., Jr (2020). Epidemiology and clinical features of COVID-19: A review of current literature. Journal of clinical virology : the official publication of the Pan American Society for Clinical Virology, 127, 104357. https://doi.org/10.1016/j.jcv.2020.104357
Hu, B., Huang, S., & Yin, L. (2021). The cytokine storm and COVID‐19. Journal of medical virology, 93(1), 250-256.
Santa Cruz, A., Mendes-Frias, A., Oliveira, A. I., Dias, L., Matos, A. R., Carvalho, A., Capela, C., Pedrosa, J., Castro, A. G., & Silvestre, R. (2021). Interleukin-6 Is a Biomarker for the Development of Fatal Severe Acute Respiratory Syndrome Coronavirus 2 Pneumonia. Frontiers in immunology, 12, 613422. https://doi.org/10.3389/fimmu.2021.613422
Bland, J. M., & Altman, D. G. (1986). Statistical methods for assessing agreement between two methods of clinical measurement. Lancet (London, England), 1(8476), 307–310.
Passing, H., & Bablok (1983). A new biometrical procedure for testing the equality of measurements from two different analytical methods. Application of linear regression procedures for method comparison studies in clinical chemistry, Part I. Journal of clinical chemistry and clinical biochemistry. Zeitschrift fur klinische Chemie und klinische Biochemie, 21(11), 709–720. https://doi.org/10.1515/cclm.1983.21.11.709
Passing, H., & Bablok, W. (1984). Comparison of several regression procedures for method comparison studies and determination of sample sizes. Application of linear regression procedures for method comparison studies in Clinical Chemistry, Part II. Journal of clinical chemistry and clinical biochemistry. Zeitschrift fur klinische Chemie und klinische Biochemie, 22(6), 431–445. https://doi.org/10.1515/cclm.1984.22.6.431